Durch einen Kommilitonen bin ich auf die Idee gekommen die Laufzeiten meines multithreaded RT-Algorithmus mittels gnuplot zu visualisieren; zur Einführung in gnuplot bitte diesen Link beachten.
gnuplot ist ein Funktionsplotter, kann aber nicht nur Funktionen sondern auch einfache Punkte auf einem Koordinatensystem visualisieren und miteinander verbinden. Wenn Ihr es bei euch installiert solltet Ihr den Installer von der Homepage nehmen und dabei zwei Dinge beachten: Zum einen sollte der gnuplot-Programmpfad der Windows-PATH-Variable hinzugefügt werden und zum anderen sollte der Terminal-Typ auf Windows gesetzt werden.
Ich habe meine Variante drei vom multithreaded RT-Algorithmus genommen und die Laufzeitmessungen von JAMon auf die Visualisierung mittels gnuplot vorbereitet. Dazu gehörten die Einführung der neuen Variablen Startmenge, Schrittweite und Schritte - statt wie bislang Einzelmessungen durchzuführen werden in dieser Variante Mehrfachmessungen durchgeführt.
Einige Sachen habe ich weggekürzt wie die Laufzeitmessung für das Zeichnen, aber auch die initialen Prüfungen ob die Zufallszahlenmenge groß genug für diese Anzahl Knoten ist.
Die Ergebnisse werden gesammelt und in die Datei gnuplot.dat geschrieben - sowie die Kommandodatei gnuplot.bat erstellt welche darauf verweist und Instruktionen für gnuplot bereithält wie z. B. Achsenbeschriftungen, aber auch die x- und y-Skalen.
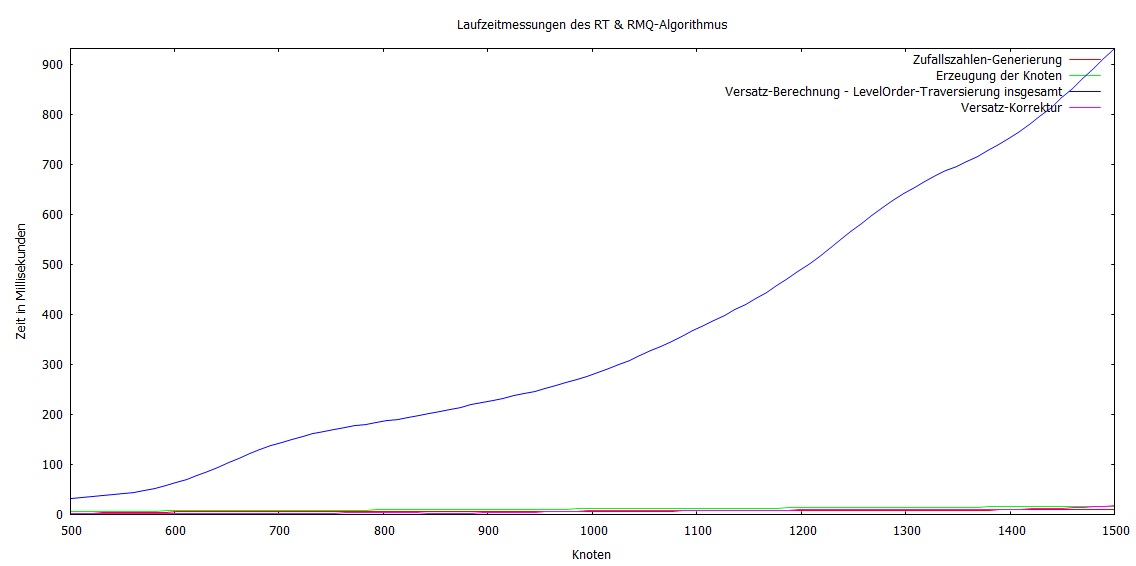
Nachfolgend die Ergebnisse der Knotenmengen 500 - 1500 mit der Schrittweite 100 - absichtlich gering gewählt damit es schnell ging. Für repräsentativere Laufzeitergebnisse bitte die anderen Beiträge lesen oder selber messen.
Die akkumulierten Gesamtzeiten werden übrigens abschließend auf der Konsole ausgegeben.
Update 14.01.2012: Es ist bei der Zufallszahlengenerierung sinnvoller den Iterator als generischen Typ anzulegen:
Iterator<Integer> it = Zufallszahlen.iterator();
Dadurch spart man sich beim Durchlauf den expliziten Integer-Cast vor dem it.next()-Befehl.
Außerdem habe ich nun gemäß dem Ubuntuusers-Wiki-Eintrag zu gnuplot mit der Verwendung des Minus - Parameters erreicht dass gnuplot nach dem Schließen des Plot-Fensters in den interaktiven Modus wechselt. Gnuplot wird dadurch nun automatisch beendet sobald das Processing-Programm geschlossen wird und verbleibt nicht mehr im Arbeitsspeicher.
Ergänzung 15.01.2012: Durch das fehlende Zeichnen verwende ich nun eigentlich gar keine Spezialitäten von Processing mehr, der Quellcode unten müsste sich daher nahezu 1:1 in Eclipse/Java übernehmen lassen - da Processing auf Java basiert.
Ergänzung 27.02.2012: Gnuplot berechnet Näherungswerte zwischen den Punkten, ansonsten würden Zick-Zack-Linien entstehen. Im Beispiel unten verwende ich den Modus csplines, aber es gibt u. a. auch noch die Möglichkeit der Bezier-Kurven, womit die Statistik meinem damaligen Test zufolge noch linearer erscheint.
Wenn man das weiter ausbauen will wäre es sicher sinnvoll die Annäherungsmodi von gnuplot als Parameter an die Routine zu übergeben, wobei man dann String als Datentyp vermeiden und z. B. Enumerationen verwenden könnte.
/************************************************************************************
Laufzeitmessung des RT/RMQ-Algorithmus in Processing
- und Monitoring via JAMon -
- und Ausgabe über gnuplot -
von Thomas Kramer
Version 1.56 - 14.01.2012
************************************************************************************/
/* Konfiguration */
int startMenge = 500;
int schrittWeite = 100;
int schritte = 10;
/* RMQ-Abfragen einschalten? */
boolean RMQ_Abfragen = false;
/* Zufallszahlen-Unter-/Oberwert festlegen */
int unten = 1;
int oben = 100000000;
/* Farben festlegen */
color c3 = color(193, 185, 185);
/* Konfiguration-Ende */
/* weitere globale Variablen */
int Ebene = 0;
int EbenenInsgesamt = 0;
tBaum Wurzel = null;
tBaum kleinster_Versatz = null;
tBaum groesster_Versatz = null;
tBaum letzter_Knoten = null;
tBaum[] RMQ_E = null;
int[] RMQ_L = null;
int[] RMQ_R = null;
HashSet<Integer> Zufallszahlen = new HashSet<Integer>();
ArrayList<tBaum> ZList = new ArrayList<tBaum>();
Hashtable<Integer, Pointer_Class> LevelTable = new Hashtable<Integer, Pointer_Class>();
Monitor mon1=null;
Monitor mon2=null;
Monitor mon3=null;
Monitor mon4=null;
Monitor mon5=null;
Monitor mon6=null;
Monitor mon8=null;
Monitor mon9=null;
Monitor mon10=null;
double[] resultsMon1 = null;
double[] resultsMon2 = null;
double[] resultsMon3 = null;
double[] resultsMon4 = null;
double[] resultsMon5 = null;
double[] resultsMon6 = null;
double[] resultsMon8 = null;
double[] resultsMon9 = null;
double[] resultsMon10 = null;
int Baumelemente = 0;
import java.util.HashMap;
import java.util.concurrent.TimeUnit;
import java.util.concurrent.Callable;
import java.util.concurrent.ExecutorService;
import java.util.concurrent.Executors;
import java.util.concurrent.ExecutionException;
import java.util.concurrent.TimeoutException;
import java.util.concurrent.Future;
import com.jamonapi.*;
public class tBaum
{
/* in Inhalt wird der Zufallszahlen-Wert gespeichert */
int Inhalt = 0;
/* gibt die Ebene für jeden Knoten an */
int Ebene = 0;
/* Art gibt die Position des Knotens im Verhältnis zur Wurzel an
-1 = linker Teilbaum, +1 = rechter Teilbaum */
int Art = 0;
int Versatz = 0;
/* fürs Einreihen der Knoten brauche ich Zufallszahlen für zufällige
Bäume, aber für den RMQ-Algorithmus ist das unpraktisch weil für das
R-Array Knoteninhalt und Index vertauscht werden, daher Tagging-Variable */
int tag = 0;
/* Pointer für das Traversieren */
tBaum Vater = null;
tBaum links = null;
tBaum rechts = null;
/* speichert die jeweilige Tiefe des linken und des rechten Unterbaumes */
Integer linksEbenen = 0;
Integer rechtsEbenen = 0;
public int getTag()
{
return this.tag;
}
};
/* Hilfsklasse für Levelorder-Traversierung */
/* jede Instanz beinhaltet alle Knoten einer Ebene */
public class Pointer_Class
{
ArrayList<tBaum> Liste = new ArrayList<tBaum>();
public void add(tBaum Knoten)
{
Liste.add(Knoten);
}
public ArrayList<tBaum> getList()
{
return this.Liste;
}
}
/* im linken Unterbaum muss das Maximum gefunden werden */
public class finde_linken_Versatz implements Callable
{
tBaum Knoten = null;
tBaum EndKnoten = null;
Integer bisZuEbene = 0;
Integer Versatz = 0;
/* leerer Konstruktor */
public finde_linken_Versatz()
{
}
public void setze_Daten(tBaum Knoten, Integer bisZuEbene, Integer Versatz)
{
this.Knoten = Knoten;
this.EndKnoten = Knoten;
this.bisZuEbene = bisZuEbene;
this.Versatz = Versatz;
}
/* rekursive Methode */
private Integer finde_Versatz(tBaum Knoten, Integer Versatz)
{
int result = Versatz;
if (Knoten != null)
{
result = max(Knoten.Versatz, result);
// noch nicht in der letzten zu berücksichtigenden Ebene?
if (Knoten.Ebene < this.bisZuEbene)
{
result = finde_Versatz(Knoten.links, result);
result = finde_Versatz(Knoten.rechts, result);
}
}
return result;
}
public Integer call()
{
return finde_Versatz(this.Knoten, this.Versatz);
}
}
/* im rechten Unterbaum muss das Minimum gefunden werden */
public class finde_rechten_Versatz implements Callable
{
tBaum Knoten = null;
tBaum EndKnoten = null;
int bisZuEbene = 0;
int Versatz = 0;
/* leerer Konstruktor */
public finde_rechten_Versatz()
{
}
public void setze_Daten(tBaum Knoten, Integer bisZuEbene, Integer Versatz)
{
this.Knoten = Knoten;
this.EndKnoten = Knoten;
this.bisZuEbene = bisZuEbene;
this.Versatz = Versatz;
}
/* rekursive Methode */
private Integer finde_Versatz(tBaum Knoten, Integer Versatz)
{
int result = Versatz;
if (Knoten != null)
{
result = min(Knoten.Versatz, result);
// noch nicht in der letzten zu berücksichtigenden Ebene?
if (Knoten.Ebene < this.bisZuEbene)
{
result = finde_Versatz(Knoten.links, result);
result = finde_Versatz(Knoten.rechts, result);
}
}
return result;
}
public Integer call()
{
return finde_Versatz(this.Knoten, this.Versatz);
}
}
void setup() {
/* Bildschirm löschen */
background(c3);
noLoop();
double[] resultsMon1 = new double[schritte + 1];
double[] resultsMon2 = new double[schritte + 1];
double[] resultsMon3 = new double[schritte + 1];
double[] resultsMon4 = new double[schritte + 1];
double[] resultsMon5 = new double[schritte + 1];
double[] resultsMon6 = new double[schritte + 1];
double[] resultsMon10 = new double[schritte + 1];
double minTime = 0;
double maxTime = 0;
/* Laufzeiten ermitteln */
int s = 0;
for (int i = startMenge; i <= (startMenge + (schrittWeite * schritte)); i += schrittWeite)
{
Laufzeitmessung(i);
/* für Zeitskala Maximum suchen */
/* der max-Befehl von Processing funktioniert übrigens nur mit Ganzzahlen und kann
hier nicht verwendet werden */
resultsMon1[s] = mon1.getTotal();
if (resultsMon1[s] > maxTime)
{
maxTime = resultsMon1[s];
}
resultsMon2[s] = mon2.getTotal();
if (resultsMon2[s] > maxTime)
{
maxTime = resultsMon2[s];
}
resultsMon3[s] = mon3.getTotal();
if (resultsMon3[s] > maxTime)
{
maxTime = resultsMon3[s];
}
resultsMon10[s] = mon10.getTotal();
if (resultsMon10[s] > maxTime)
{
maxTime = resultsMon10[s];
}
/* Rest optional, RMQ-Abfragen */
if (mon4 != null)
{
resultsMon4[s] = mon4.getTotal();
if (resultsMon4[s] > maxTime)
{
maxTime = resultsMon4[s];
}
}
if (mon5 != null)
{
resultsMon5[s] = mon5.getTotal();
if (resultsMon5[s] > maxTime)
{
maxTime = resultsMon5[s];
}
}
if (mon6 != null)
{
resultsMon6[s] = mon6.getTotal();
if (resultsMon6[s] > maxTime)
{
maxTime = resultsMon6[s];
}
}
s++;
}
String aktVerzeichnis = System.getProperty("user.dir");
aktVerzeichnis = aktVerzeichnis.replace("\\","/");
if (aktVerzeichnis.substring(aktVerzeichnis.length()-1) != "/")
aktVerzeichnis += "/";
/* Dateinamen festlegen */
String batfile = aktVerzeichnis + "gnuplot.bat";
String datfile = aktVerzeichnis + "gnuplot.dat";
/* Kommandodatei für gnuplot schreiben */
PrintWriter output = createWriter(batfile);
output.println("# Laufzeitmessungen");
output.println("#====================================");
output.println("set title 'Laufzeitmessungen des RT & RMQ-Algorithmus'");
String test = String.format("set yrange [%f:%f]\n", minTime, maxTime).replace(",",".");
output.printf(test, minTime, maxTime);
output.printf("set xrange [%d:%d]\n", startMenge, startMenge + (schrittWeite * schritte));
output.println("set xlabel 'Knoten'");
output.println("set ylabel 'Zeit in Millisekunden'");
output.printf("plot '%s' using 1:2 smooth csplines title 'Zufallszahlen-Generierung', ", datfile);
output.printf(" '%s' using 1:3 smooth csplines title 'Erzeugung der Knoten', ", datfile);
output.printf(" '%s' using 1:4 smooth csplines title 'Versatz-Berechnung - LevelOrder-Traversierung insgesamt', ", datfile);
output.printf(" '%s' using 1:5 smooth csplines title 'Versatz-Korrektur'", datfile);
if (RMQ_Abfragen)
{
output.printf(", '%s' using 1:6 smooth csplines title 'Euler-Tour'", datfile);
output.printf(", '%s' using 1:7 smooth csplines title 'RMQ-Arrays erstellen'", datfile);
output.printf(", '%s' using 1:8 smooth csplines title 'RMQ-Abfragen beantworten'", datfile);
}
// output.printf("\npause -1 '%s' \n", "Hit return to continue");
output.flush();
output.close();
/* Datendatei für gnuplut schreiben */
s = 0;
PrintWriter outputDatfile = createWriter(datfile);
for (int i = startMenge; i <= (startMenge + (schrittWeite * schritte)); i += schrittWeite)
{
outputDatfile.printf("%d ", i);
outputDatfile.printf("%f ", resultsMon1[s]);
outputDatfile.printf("%f ", resultsMon2[s]);
outputDatfile.printf("%f ", resultsMon3[s]);
outputDatfile.printf("%f ", resultsMon10[s]);
if (RMQ_Abfragen)
{
outputDatfile.printf("%f ", resultsMon4[s]);
outputDatfile.printf("%f ", resultsMon5[s]);
outputDatfile.printf("%f ", resultsMon6[s]);
}
outputDatfile.printf("\n");
s++;
}
outputDatfile.flush();
outputDatfile.close();
/* gnuplot starten */
String[] params = { "gnuplot.exe", "-e", "load '" + batfile + "'", "-"};
open(params);
/* akkumulierte Zeiten auf der Konsole ausgeben */
ausgabeZeit();
}
void Laufzeitmessung(int anzahlKnoten)
{
Baumelemente = anzahlKnoten;
/*-----------------------------------------------------------------------------
* einmalige Zufallszahlen erzeugen
*-----------------------------------------------------------------------------*/
mon1=MonitorFactory.start("Zufallszahlen-Generierung");
Zufallszahlen = new HashSet<Integer>();
while (Zufallszahlen.size() < Baumelemente)
Zufallszahlen.add((int) random(unten, oben));
mon1.stop();
/*-----------------------------------------------------------------------------
* Knoten erzeugen
*-----------------------------------------------------------------------------*/
mon2=MonitorFactory.start("Erzeugung der Knoten");
int i = 0;
Iterator<Integer> it = Zufallszahlen.iterator();
ZList = new ArrayList<tBaum>();
while (it.hasNext())
{
if (i == 0)
{
Wurzel = Einfuegen(null, null, it.next(), 0, i);
/* Initialisierungswerte setzen */
kleinster_Versatz=Wurzel;
groesster_Versatz=Wurzel;
}
else {
Einfuegen(Wurzel, null, it.next(), 0, i);
ZList.add(letzter_Knoten);
}
i++;
}
mon2.stop();
/*-----------------------------------------------------------------------------
* Versatz berechnen
*-----------------------------------------------------------------------------*/
mon3=MonitorFactory.start("Versatz-Berechnung - LevelOrder-Traversierung insgesamt");
LevelOrder();
/* kleinsten Versatz im Baum allen Knoten aufaddieren, danach hat man
die konkrete Spaltenzahl (x-Koordinate) für jeden Knoten - beginnend mit 1 */
int GesamtVersatz=abs((kleinster_Versatz).Versatz)+1;
setze_Wert(Wurzel, GesamtVersatz);
mon3.stop();
/*-----------------------------------------------------------------------------
* Euler-Tour-Arrays erstellen
*-----------------------------------------------------------------------------*/
if (RMQ_Abfragen)
{
/* Startzeit nehmen */
mon4=MonitorFactory.start("Euler-Tour");
RMQ_E = new tBaum[(2*anzahlKnoten)-1];
RMQ_L = new int [(2*anzahlKnoten)-1];
RMQ_R = new int [anzahlKnoten];
Euler_Tour(Wurzel,-1);
mon4.stop();
mon5=MonitorFactory.start("RMQ-Arrays erstellen");
fillRMQ_R_Array();
mon5.stop();
/*-----------------------------------------------------------------------------
* RMQ-Abfragen beantworten
*-----------------------------------------------------------------------------*/
/* Zuerst Liste mit Knoten shufflen */
Collections.shuffle(ZList);
/* Startzeit nehmen */
mon6=MonitorFactory.start("RMQ-Abfragen beantworten");
int tag1 = 0;
int tag2 = 0;
int result = 0;
i = 0;
/* Wurzelknoten wurde ja nicht einbezogen, also Obergrenze = Anzahl -2 */
int x = Baumelemente -2;
/* soviele Abfragen beantworten wie Knoten-1 da sind */
while (x >= 0)
{
tag1 = ZList.get(i).tag;
tag2 = ZList.get(x).tag;
/* bei Performance-Tests wollen wir die Zeit für die Bildschirmausgabe nicht mittesten */
/* println("LCA von " + tag1 + " und " + tag2 + " = " + LCA(tag1, tag2).tag); */
result = LCA(tag1, tag2).tag;
i++;
x--;
}
/* Endzeit nehmen und Ausgabe */
mon6.stop();
}
}
/* addiere den nach der Formel korrigierten Versatz jedem einzelnen
Knoten der angegebenen Kontur auf */
void setze_Wert(tBaum Knoten, int Wert)
{
if (Knoten!=null)
{
Knoten.Versatz += Wert;
setze_Wert(Knoten.links,Wert);
setze_Wert(Knoten.rechts,Wert);
}
}
/* Einfügen der Knoten, Position wird in der Routine selbst bestimmt */
tBaum Einfuegen(tBaum Knoten, tBaum Vater, int Inhalt, int Versatz, int tag)
{
Pointer_Class KnotenMengeProEbene = null;
if (Knoten == null)
{
/* angegebener Knoten existiert noch nicht (Position noch nicht belegt)
--> neuen Knoten erzeugen */
Knoten = new tBaum();
Knoten.Vater = Vater;
Knoten.links = null;
Knoten.rechts = null;
Knoten.Inhalt = Inhalt;
Knoten.Ebene = Ebene+1;
Knoten.tag = tag;
/* Versatz mit Initialisierungswerten versehen */
Knoten.Versatz = Versatz;
EbenenInsgesamt = max(EbenenInsgesamt, Knoten.Ebene);
/* Position im Baum abhängig zur Wurzel bestimmen */
Knoten.Art=0;
if (Wurzel != null)
{
Knoten.Art = (Inhalt < Wurzel.Inhalt) ? -1 : +1;
/* kleinsten/größten Versatz bestimmen */
if (Knoten.Versatz < (kleinster_Versatz).Versatz)
kleinster_Versatz = Knoten;
if (Knoten.Versatz > (groesster_Versatz).Versatz)
groesster_Versatz = Knoten;
}
/* nimm alle Knoten von der aktuellen Ebene aus dem Hashtable */
KnotenMengeProEbene = LevelTable.get(Knoten.Ebene);
/* wenn noch nicht gespeichert neu instanziieren */
if (KnotenMengeProEbene == null)
KnotenMengeProEbene = new Pointer_Class();
/* füge dieser Menge den aktuellen Knoten hinzu */
KnotenMengeProEbene.add(Knoten);
/* speichere diese Menge wieder in dem Hashtable */
LevelTable.put(Knoten.Ebene, KnotenMengeProEbene);
letzter_Knoten = Knoten;
} else
{
Ebene += 1;
if (Inhalt < Knoten.Inhalt)
{ /* kleineren Wert als den des aktuellen Knotens immer als linken Sohn einfügen */
Knoten.links = Einfuegen(Knoten.links, Knoten, Inhalt, Versatz-1, tag);
Knoten.linksEbenen = max(Knoten.linksEbenen, letzter_Knoten.Ebene);
}
else if (Inhalt > Knoten.Inhalt)
{ /* größeren Wert als den des aktuellen Knotens immer als rechten Sohn einfügen */
Knoten.rechts = Einfuegen(Knoten.rechts, Knoten, Inhalt, Versatz+1, tag);
Knoten.rechtsEbenen = max(Knoten.rechtsEbenen, letzter_Knoten.Ebene);
}
Ebene -= 1;
}
return Knoten;
}
/* Startwert sollte bei -1 liegen */
int Euler_Tour(tBaum Knoten, int Zaehler)
{
if (Knoten!=null)
{
Zaehler+=1;
RMQ_E[Zaehler]=Knoten;
RMQ_L[Zaehler]=Knoten.Ebene-1;
if (Knoten.links!=null)
{
Zaehler=Euler_Tour(Knoten.links, Zaehler)+1;
RMQ_E[Zaehler]=Knoten;
RMQ_L[Zaehler]=Knoten.Ebene-1;
}
if (Knoten.rechts!=null)
{
Zaehler=Euler_Tour(Knoten.rechts, Zaehler)+1;
RMQ_E[Zaehler]=Knoten;
RMQ_L[Zaehler]=Knoten.Ebene-1;
}
}
return Zaehler;
}
/* fülle Repräsentanten-Array, welche das erste Vorkommen jedes Knotens enthält */
void fillRMQ_R_Array()
{
/* RMQ_R füllen. Dazu alle Knoten durchgehen... */
int s=0;
for (int r=0; r<Baumelemente; r+=1)
{
/* ... und für jeden Knoten den ersten Eintrag im RMQ_E-Array finden ... */
for (s=0; s<(Baumelemente*2-1); s+=1)
{
if (RMQ_E[s].tag == r)
break;
}
RMQ_R[r]=s;
}
}
/* mittels RMQ-Algorithmus den Lowest Common Ancestor ermitteln */
tBaum LCA(int tag1, int tag2)
{
/* Suche im RMQ_R-Array zunächst die Entsprechung für tag1 und tag2 der beiden
ausgewählten Knoten aus, suche dann innerhalb dieser Grenzen im RMQ_L-Array
den niedrigsten Wert heraus.
Anschließend wird im RMQ_E-Array der Wert aus dieser Indexposition zurückgegeben */
int lowest=Baumelemente;
int lowest_index=0;
tBaum result=null;
for (int i=min(RMQ_R[tag1], RMQ_R[tag2]); i<=max(RMQ_R[tag1], RMQ_R[tag2]); i+=1)
{
if (RMQ_L[i]<lowest)
{
lowest=RMQ_L[i];
lowest_index=i;
}
}
/* Default-Rückgabewert setzen gemäß Algorithmus */
result = RMQ_E[lowest_index];
/* wenn Knoten B ein Sohn von A ist wird A gemäß Algorithmus zurückgeliefert,
dann greift Ausnahmeregelung */
if ((RMQ_E[lowest_index].tag == tag1) || (RMQ_E[lowest_index].tag == tag2))
if (RMQ_E[lowest_index].Vater != null )
result = RMQ_E[lowest_index].Vater;
return result;
}
/* starte Levelorder-Traversierung */
void LevelOrder()
{
ExecutorService executor = Executors.newCachedThreadPool();
Pointer_Class KnotenMengeProEbene = null;
ArrayList KnotenMengeProEbene2 = null;
tBaum Knoten[] = null;
finde_linken_Versatz a[] = null;
finde_rechten_Versatz b[] = null;
int minLevelinsgesamt = 0;
Future<Integer> erg1[] = null;
Future<Integer> erg2[] = null;
int Versatz = 0;
Integer linke_Kontur = 0;
Integer rechte_Kontur = 0;
int threadsA = 0;
int threadsB = 0;
int threadsAMax = 0;
int threadsBMax = 0;
int i = 0;
int x = 0;
i = EbenenInsgesamt -1;
while (i >= 1)
{
/* nimm alle Knoten von der aktuellen Ebene aus dem Hashtable */
KnotenMengeProEbene = LevelTable.get(i);
KnotenMengeProEbene2 = KnotenMengeProEbene.getList();
x = 0;
Knoten = new tBaum[KnotenMengeProEbene2.size()];
a = new finde_linken_Versatz[KnotenMengeProEbene2.size()];
b = new finde_rechten_Versatz[KnotenMengeProEbene2.size()];
erg1 = new Future[KnotenMengeProEbene2.size()];
erg2 = new Future[KnotenMengeProEbene2.size()];
threadsA = 0;
threadsB = 0;
while (x < KnotenMengeProEbene2.size())
{
Knoten[x] = (tBaum) KnotenMengeProEbene2.get(x);
minLevelinsgesamt=min(Knoten[x].linksEbenen, Knoten[x].rechtsEbenen);
/* bestimme den maximalen und minimalen Versatz jeder Kontur bis zu der bestimmten Ebene (einschließlich) */
/* starte dazu soviele Threads wie Knoten in der Ebene vorhanden sind */
/* das gilt aber nur für jeden Knoten, der beide Söhne hat */
if ((Knoten[x].links != null) && (Knoten[x].rechts != null))
{
a[x] = new finde_linken_Versatz();
mon8=MonitorFactory.start("Multithreading - finde max im linken Unterbaum");
a[x].setze_Daten(Knoten[x].links, minLevelinsgesamt, (Knoten[x].links).Versatz);
erg1[x] = executor.submit(a[x]);
threadsA++;
threadsAMax = max(threadsAMax, threadsA);
b[x] = new finde_rechten_Versatz();
mon9=MonitorFactory.start("Multithreading - finde min im rechten Unterbaum");
b[x].setze_Daten(Knoten[x].rechts, minLevelinsgesamt, (Knoten[x].rechts).Versatz);
erg2[x] = executor.submit(b[x]);
threadsB++;
threadsBMax = max(threadsBMax, threadsB);
}
x++;
}
/* warte auf das Ergebnis der Threads, indem die Ergebnisse ausgelesen werden */
try
{
x = 0;
while (x < KnotenMengeProEbene2.size())
{
if ((Knoten[x].links != null) && (Knoten[x].rechts != null))
{
linke_Kontur = erg1[x].get();
mon8.stop();
threadsA--;
rechte_Kontur = erg2[x].get();
mon9.stop();
threadsB--;
/* Korrigierungs-Versatz berechnen */
Versatz=(linke_Kontur - rechte_Kontur) +2;
/* Ergebnis ist ungerade? */
if ((Versatz & 1) != 0)
Versatz += 1;
/* Integer-Division */
Versatz=(Versatz / 2);
/* diesen Versatz dem linken Teilbaum als negativen Wert aufaddieren, dem rechten Teilbaum
als positiven Wert */
mon10=MonitorFactory.start("Versatz-Korrektur");
setze_Wert(Knoten[x].links,Versatz * -1);
setze_Wert(Knoten[x].rechts,Versatz);
mon10.stop();
}
x++;
}
}
catch (ExecutionException ex)
{}
catch (InterruptedException ex)
{}
i--;
}
executor.shutdown();
}
/* Zeitmessung ausgeben */
void ausgabeZeit()
{
if (mon1 != null)
println(mon1 + "\n");
if (mon2 != null)
println(mon2 + "\n");
if (mon3 != null)
println(mon3 + "\n");
if (mon4 != null)
println(mon4 + "\n");
if (mon5 != null)
println(mon5 + "\n");
if (mon6 != null)
println(mon6 + "\n");
if (mon8 != null)
println(mon8 + "\n");
if (mon9 != null)
println(mon9 + "\n");
if (mon10 != null)
println(mon10 + "\n");
}