Wie bereits angekündigt habe ich mittlerweile den Range-Minimum-Query-Algorithmus in mein Binärbaum-Programm implementiert. Der RMQ-Algorithmus ist eine neuere Alternative zum Algorithmus von Schieber und Vishkin.
Verweisen möchte ich auf die vorherige Version des Programmes, dort befinden sich auch die recherchierten Quellen zum Reingold-Tilford-Algorithmus. Im Vergleich zur bisherigen Version habe ich den Traversierungscode entfernt, da das Programm sonst zu unübersichtlich wird – Processing unterstützt leider kein Codefolding oder ein direktes Anspringen von Routinen.
Da ich weiterhin Zufallsbäume haben wollte musste ich zuerst überlegen wie ich den RMQ-Algorithmus implementiere, denn für das RMQ_R-Array werden Inhalt und Indexposition der Knoten vom RMQ_E-Array miteinander vertauscht, was bei meinen bisherigen Zufallszahlen von 1-65535 eher unpraktisch war (zudem genaugenommen nicht eindeutig).
Andererseits wollte ich auch nicht die Einfügemethodik ändern – es handelt sich ja um ein Binärbaum-Programm – und so kam ich auf die Idee die Zufallszahlen beizubehalten (anhand derer der Baum zufällig aufgebaut wird), aber gleichzeitig einen Tag-Code für jeden Knoten einzuführen.
Diese Tag-Codes sind nun fortlaufende Zahlen - anhand zweier dieser Codes werden zwei Knoten eindeutig identifiziert, worüber die LCA-Routine den tiefsten gemeinsamen Vorfahren bestimmt. Zu diesem Zweck habe ich auch eine Konsolenausgabe eingebaut, über die der Inhalt der Arrays RMQ_E, RMQ_L und RMQ_R ausgegeben wird und mithilfe derer die Richtigkeit überprüft werden kann.
Orientiert habe ich mich bei der Implementierung hauptsächlich an dem Script Algorithmen zum Ermitteln des Lowest Common Ancestor (LCA) von Ingo Mohr, aber auch im Script Algorithmen auf Sequenzen der Ludwig-Maximilians-Universität München sind dem Range-Minimum-Query-Algorithmus Kapitel gewidmet. Dieser Algorithmus funktioniert folgendermaßen:
Zunächst werden drei Arrays erstellt, RMQ_E, RMQ_L und RMQ_R. Das RMQ_E-Array enthält Verweise auf jeden einzelnen Knoten und wird in der Reihenfolge gemäß der Euler-Tour gefüllt. Zugleich wird das RMQ_L-Array gefüllt mit den Level-Angaben jedes Knotens der Euler-Tour. Diese beiden Arrays benötigen eine Länge von 2*Anzahl Baumelemente-1. Danach wird das RMQ_R-Array gefüllt mit der ersten Position jedes Knotens im RMQ_E-Array, nur das hier Inhalt (tag) und Index-Position vertauscht werden - für dieses Array wird natürlich eine Länge gemäß der Anzahl Baumelemente benötigt.
Der LCA()-Funktion werden die tag-Codes zweier Knoten übergeben. Anschließend funktioniert die Suche folgendermaßen: Zuerst werden aus dem RMQ_R-Array aus der Indexposition der übergebenen Tag-Werte die resultierenden Werte herausgesucht, danach wird im RMQ_L-Array innerhalb dieser beiden Indexpositionen der niedrigste Wert und dessen Indexposition bestimmt - an dieser Position befindet sich im RMQ_E-Array der Lowest Common Ancestor, der niedrigste gemeinsame Vorfahre zweier Knoten im Baum.
Der Einfachheit halber habe ich fünf LCA()-Abfragen hartkodiert eingebaut - das Ergebnis wird natürlich schon berechnet - daher sollte die Anzahl Knoten nicht auf weniger als 10 eingestellt werden.
Im Script der LM-Universität München wird auch eine schnellere Abarbeitung des RMQ-Algorithmus mithilfe von Lookup-Tabellen erläutert – vergleiche dazu Kapitel 4.1.4 bis 4.1.5 mit den Abschnitten Naiver Lösungsansatz für RMQ-Abfrage in O(1) und Schnellerer Algorithmus im Script von Ingo Mohr.
Update 04.10.2011: Mittlerweile habe ich in der LCA-Routine eine Sonderbehandlung eingebaut für den Fall das Knoten B ein Sohn von A ist, in dieser Situation soll nicht mehr Knoten A zurückgegeben werden sondern der Vater von A. Das steht aber im Einklang zum Algorithmus, dieser liefert eben das Ergebnis in dem Falle – hierbei handelt es sich um keinen Implementierungsfehler.
Außerdem hatte unser Dozent mal gesagt das es nur einen Ausgang in einer Funktion geben sollte, daher habe ich auch das ganze Programm diesbezüglich nochmal angepasst. Zusätzliche Abbruchbedingungsprüfungen am Anfang einer Funktion - ohne das sie mit if-Abfragen durchgeschleift werden - finde ich aber grundsätzlich in Ordnung.
Update 17.10.2011: Statt einer Multiplikation mit -1 ist natürlich die Nutzung der abs()-Funktion eleganter, um den Betrag zu ermitteln. Außerdem habe ich nun die min()- und max()-Funktionen konsequenter eingesetzt, um mehr if-Abfragen einzusparen.
Update 28.12.2011: Änderungen beim RT-Algorithmus: Es werden nun einmalige Zufallszahlen generiert. Dazu verwende ich ein HashSet, welches die Eigenschaft hat keine doppelten Einträge aufnehmen zu können. Dieses fülle ich solange mit Zufallszahlen bis seine Größe der eingestellten Anzahl Knoten entspricht.
Danach gehe ich mit einem Iterator durch die Datenmenge im Hashset und erzeuge jedes Mal einen neuen Knoten mit dieser Zufallszahl.
Daher sollten nun immer soviele Knoten erzeugt werden wie eingestellt, weil doppelte Zufallszahlen nun vermieden werden. Voraussetzung ist aber dass die eingestellte Anzahl Knoten kleiner als das Zufallszahlen-Intervall ist. Zu diesem Zweck führe ich nun ganz zu Beginn eine Sicherheitsabfrage durch. Damit die Geschwindigkeit nicht zu sehr leidet sollte das Zufallszahlen-Intervall natürlich deutlich größer als die Knotenanzahl sein.
Die Modulo-Abfrage wird nun bitweise mit dem &-Operator durchgeführt, weil das so schneller ist - und ich habe eine Menge redundanter Berechnungen in der Draw-Routine entfernt. Mittlerweile habe ich auch mit über einer Million Knoten getestet und kann mit Gewissheit sagen, dass bei der Berechnung des Korrektur-Versatzes nicht die abs()-Funktion benutzt werden muss.
Update 29.12.2011: Änderungen beim RT-Algorithmus: Eine Kontrollfunktion hinzugefügt die überprüft ob bereits ein Knoten an die gleiche Position gezeichnet wurde, entsprechende Knoten rot hervorhebt und auf der Konsole ausgibt. Außerdem wird nun aus Geschwindigkeitsgründen eine Warnung ausgegeben, falls die Knotenanzahl nicht mindestens 20% kleiner als das Zufallszahlen-Intervall ist.
Nun habe ich auch die Geschwindigkeit des Algorithmus verbessert, indem ich die Tiefe des linken und rechten Unterbaumes jedes Knotens bereits beim Erzeugen der Knoten speichere - natürlich muss das dann aber auch beim Löschen von Knoten berücksichtigt werden, daher habe ich die Routine finde_Max_Ebene() vorerst drin gelassen. Leider funktioniert das nicht entsprechend bei der Findung des minimalen und maximalen Versatzes - für diesen Fall wäre Multithreading-Programmierung einmal angebracht.
Nachfolgend habe ich außerdem Laufzeittests der beiden Algorithmen durchgeführt - Testsystem ist ein fünf Jahre altes Turion 64x2 1,6 GHZ-Notebook:
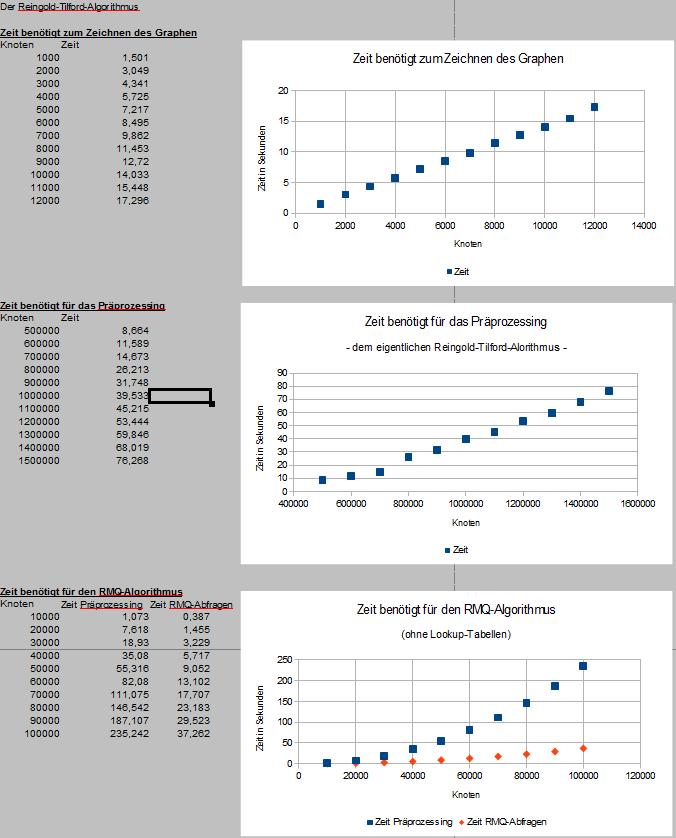
Ohne Lookup-Tabellen arbeitet der RMQ-Algorithmus bekanntermaßen nicht in konstanter Zeit. Die Anzahl Abfragen entsprach dabei jeweils der Anzahl Knoten -1 (Wurzelknoten nicht berücksichtigt). Dabei wurden alle Knoten zusätzlich in einer Arraylist zwischengespeichert, durchgemischt und dann in einer Schleife sowohl von oben als auch von unten jeweils ein Knoten genommen und darüber der LCA bestimmt.
Update 30.12.2011: Aus dem oben erwähnten Skript "Algorithmen auf Sequenzen" wurde nicht genau ersichtlich wo der Algorithmus von Bender und Farach-Colton nun beginnt und endet - es wurden mehrere Algorithmen vorgestellt. Gemäß der Bachelor-Arbeit von Umingo.de beginnt er mit dem Konstrukt des Kartesischen Baumes, also siehe Kapitel 4.1.8 im Skript "Algorithmen auf Sequenzen".
Der oben vorgestellte RMQ-Algorithmus funktioniert auch, er ist nur mit einer Vorverarbeitungszeit von O(n + p(2n-1)) und einer Abfragezeit von O(q(2n - 1)) etwas langsam - vergleiche Lemma 4.4 im Skript "Algorithmen auf Sequenzen" (Seite 118). Im Skript von Ingo Mohr steht auf Seite 7 dasselbe, er hat es nur mit f- und g-Funktion minimal anders ausgedrückt.
Praktisch ergibt sich daraus dass für das Präprozessing des RMQ-Algorithmus bei einer Verdopplung der Anzahl Knoten sich die benötigte Zeit mehr als vervierfacht -> n=2x (Verdopplung), 2n ist dann also 2*2=4. Bei der O-Notation kann man zwar die unwesentlichen Faktoren weglassen, O(2n) als Angabe würde aber eine Linearität suggerieren die in Wirklichkeit nicht gegeben ist für das Präprozessing.
Für die eigentlichen RMQ-Abfragen trifft hingegen O(2n) zu.
Update 31.12.2011: Änderungen beim RT-Algorithmus: Der minimale Versatz im Baum wird nun ebenfalls bereits beim Erzeugen der Knoten zwischengespeichert - als Pointer (Werte werden ja nachfolgend noch korrigiert). Dadurch wurde aber praktisch keine Performance-Verbesserung erreicht, da das auch nachträglich bereits sehr schnell bestimmt wurde.
In der anderen Version habe ich nun die Möglichkeit eingebaut im Zentrierungsmodus per Cursortasten den Fokus zu verschieben bzw. zu scrollen. Das passt in diese Variante nicht hinein, weil ich hier wegen der Laufzeitmessungen das wiederholte Zeichnen abschalten lasse.
Update 02.01.2012: Änderungen beim RT-Algorithmus: Es kann ein vollständiger Rekursionsdurchlauf eingespart werden wenn die Regel Nr. 5. beim RT-Algorithmus direkt in der Zeichnen-Routine geschieht - beim erneuten Zeichnen darf es dann aber natürlich nicht erneut aufaddiert werden.
Das habe ich heute umgesetzt, allerdings wird dann natürlich ein Teil des RT-Algorithmus bei der Laufzeitmessung nicht mehr mitgemessen - daher habe ich das alte Code-Fragment nur auskommentiert und nicht entfernt.
Update 27.01.2012: Ein paar Multiplikationen bzw. Divisionen würden sich noch durch Bitschiebeoperationen optimieren lassen, aber diese minimale Änderung nehme ich nun nicht mehr vor.
Update 04.02.2012: Das Minimum bzw. Maximum zweier Integers lässt sich durch Binär-Tricks angeblich auch schneller folgendermaßen herausfinden:
Minimum:
int x;
// we want to find the minimum of x and y
int y;
int r; // the result goes here
r = y ^ ((x ^ y) & -(x < y)); // min(x, y)
Maximum:
r = x ^ ((x ^ y) & -(x < y)); // max(x, y)
Quelle: Link. Aber das habe ich nicht getestet und werde ich auch nicht mehr einbauen. Zudem leidet darunter die Lesbarkeit und vielleicht funktioniert das auch nur unter C(++).
Fortsetzung: Link.
Weitere Links:
- Bachelor-Arbeit auf Umingo.de zum Algorithmus von Bender und Farach-Colton: Link
- Algorithm Tutorials: Range Minimum Query and Lowest Common Ancestor: Link
- - "The LCA Problem Revisited" [PPT] by Michael A.Bender and Martin Farach-Colton
/************************************************************************************
Visualisierung eines binären Suchbaumes in Processing
mithilfe des Reingold-Tilford-Algorithmus
und Suche des LCA über den RMQ-Algorithmus
von Thomas Kramer
Version 1.40 - 14.08.2012
************************************************************************************/
/* Konfiguration */
int Baumelemente = 20;
/* wenn Zentrierung aktiviert wird, werden die Mausabfragen deaktiviert */
boolean Zentrierung = true;
/* RMQ-Abfragen einschalten? */
boolean RMQ_Praeprocessing = true;
boolean RMQ_Abfragen = false;
/* debugging-Ausgabe */
boolean debug = true;
/* für Laufzeittests kann es sinnvoll sein das Zeichnen generell zu unterdrücken */
boolean zeichnen = false;
/* Zufallszahlen-Unter-/Oberwert festlegen */
int unten = 1;
int oben = 100000000;
int AbstandOben = 50;
int AbstandLinks = 10;
int ZwischenAbstandOben = 25;
int ZwischenAbstandLinks = 5;
int Breite = 160;
int Hoehe = 50;
/* Farben festlegen (Schwarz, Weiss, Hintergrund-Farbe) */
color c1 = color(0, 0, 0);
color c2 = color(255, 255, 255);
color c3 = color(193, 185, 185);
color c4 = color(245, 7, 7);
/* Konfiguration-Ende */
public class tBaum
{
/* in Inhalt wird der Zufallszahlen-Wert gespeichert */
int Inhalt = 0;
/* gibt die Ebene für jeden Knoten an */
int Ebene = 0;
/* Art gibt die Position des Knotens im Verhältnis zur Wurzel an
-1 = linker Teilbaum, +1 = rechter Teilbaum */
int Art = 0;
int Versatz = 0;
/* fürs Einreihen der Knoten brauche ich Zufallszahlen für zufällige
Bäume, aber für den RMQ-Algorithmus ist das unpraktisch weil für das
R-Array Knoteninhalt und Index vertauscht werden, daher Tagging-Variable */
int tag = 0;
/* Pointer für das Traversieren */
tBaum Vater = null;
tBaum links = null;
tBaum rechts = null;
/* speichert die jeweilige Tiefe des linken und des rechten Unterbaumes */
Integer linksEbenen = 0;
Integer rechtsEbenen = 0;
public int getTag()
{
return this.tag;
}
};
/* weitere globale Variablen */
int Ebene = 0;
int EbenenInsgesamt = 0;
tBaum Wurzel = null;
tBaum kleinster_Versatz = null;
tBaum groesster_Versatz = null;
tBaum letzter_Knoten = null;
tBaum[] RMQ_E = new tBaum[(2*Baumelemente)-1];
int[] RMQ_L = new int [(2*Baumelemente)-1];
int[] RMQ_R = new int [Baumelemente];
HashSet<Integer> Zufallszahlen = new HashSet<Integer>();
ArrayList<tBaum> ZList = new ArrayList<tBaum>();
long completeTimeBefore = 0;
long completeTimeAfter = 0;
long completeTimeDiff = 0;
/* Variablen für das Zeichnen */
int MaxElemente = 0;
int MaxElementePlatz = 0;
int Breite_2 = Breite / 2;
int Hoehe_2 = Hoehe / 2;
int GesamtVersatz = 0;
boolean ausgegeben = false;
import java.util.HashMap;
import java.util.concurrent.TimeUnit;
void setup() {
if (Baumelemente > abs(oben - unten))
throw new IllegalArgumentException("Fehler! Es werden einmalige Zufallszahlen benötigt und die Anzahl Knoten ist größer als das Zufallszahlen-Intervall!");
if ((Baumelemente * 1.2) > abs(oben - unten))
println("Achtung, die Anzahl Baumknoten ist nicht mindestens 20% größer als das Zufallszahlen-Intervall, das kann die Geschwindigkeit deutlich herabsetzen!");
/* Größe des Screens setzen */
size(screen.width, screen.height);
/* Bildschirm löschen */
background(c3);
/*-----------------------------------------------------------------------------
* einmalige Zufallszahlen erzeugen
*-----------------------------------------------------------------------------*/
Zufallszahlen = new HashSet<Integer>();
while (Zufallszahlen.size() < Baumelemente)
Zufallszahlen.add((int) random(unten, oben));
/*-----------------------------------------------------------------------------
* Startzeit messen für RT-Algorithmus
*-----------------------------------------------------------------------------*/
completeTimeBefore = System.currentTimeMillis();
/*-----------------------------------------------------------------------------
* Knoten erzeugen
*-----------------------------------------------------------------------------*/
int i = 0;
Iterator it = Zufallszahlen.iterator();
ZList = new ArrayList<tBaum>();
while (it.hasNext())
{
if (i == 0)
{
Wurzel = Einfuegen(null, null, (Integer) it.next(), 0, i);
/* Initialisierungswerte setzen */
kleinster_Versatz=Wurzel;
groesster_Versatz=Wurzel;
}
else {
Einfuegen(Wurzel, null, (Integer) it.next(), 0, i);
ZList.add(letzter_Knoten);
}
i++;
}
/*-----------------------------------------------------------------------------
* Versatz berechnen
*-----------------------------------------------------------------------------*/
berechne_Versatz(Wurzel);
/* kleinsten Versatz im Baum allen Knoten aufaddieren, danach hat man
die konkrete Spaltenzahl (x-Koordinate) für jeden Knoten - beginnend mit 1 */
GesamtVersatz=abs((kleinster_Versatz).Versatz)+1;
/* das Aufaddieren geschieht jetzt direkt in der Zeichnen-Routine,
dadurch wird aber ein Teil des RT-Algorithmus nicht mehr mitgemessen! */
// setze_Wert(Wurzel, GesamtVersatz);
/*-----------------------------------------------------------------------------
* Endzeit messen für RT-Algorithmus
*-----------------------------------------------------------------------------*/
nimmZeit("RT-Algorithmus");
/*-----------------------------------------------------------------------------
* Variablen für das Zeichnen einmalig setzen
*-----------------------------------------------------------------------------*/
MaxElemente = (groesster_Versatz).Versatz + GesamtVersatz;
MaxElementePlatz = (MaxElemente * Breite)+((MaxElemente - 1) * ZwischenAbstandLinks);
/*-----------------------------------------------------------------------------
* Euler-Tour-Arrays erstellen
*-----------------------------------------------------------------------------*/
if (RMQ_Praeprocessing)
{
/* Startzeit nehmen */
completeTimeBefore = System.currentTimeMillis();
Euler_Tour(Wurzel,-1);
fillRMQ_R_Array();
/* Endzeit nehmen und Ausgabe */
nimmZeit("Erstellung der RMQ-Arrays");
/*-----------------------------------------------------------------------------
* Debug-Ausgabe der RMQ-Arrays
*-----------------------------------------------------------------------------*/
if (debug)
{
String DebugString1;
String DebugString2;
String DebugString3;
String DebugString4;
DebugString1="Index ";
DebugString2="RMQ_E: ";
DebugString3="RMQ_L: ";
DebugString4="RMQ_R: ";
for (int r=0; r<(Baumelemente*2-1); r+=1)
{
DebugString1+=r + ", ";
DebugString2+=RMQ_E[r].tag + ", ";
DebugString3+=RMQ_L[r] + ", ";
}
for (int r=0; r<Baumelemente; r+=1)
DebugString4+=RMQ_R[r] + ", ";
println(DebugString1);
println(DebugString2);
println(DebugString3);
println(DebugString4);
}
/*-----------------------------------------------------------------------------
* RMQ-Abfragen beantworten
*-----------------------------------------------------------------------------*/
if (RMQ_Abfragen)
{
/* Zuerst Liste mit Knoten shufflen */
Collections.shuffle(ZList);
/* Startzeit nehmen */
completeTimeBefore = System.currentTimeMillis();
int tag1 = 0;
int tag2 = 0;
int result = 0;
i = 0;
/* Wurzelknoten wurde ja nicht einbezogen, also Obergrenze = Anzahl -2 */
int x = Baumelemente -2;
/* soviele Abfragen beantworten wie Knoten-1 da sind */
while (x >= 0)
{
tag1 = ZList.get(i).tag;
tag2 = ZList.get(x).tag;
/* bei Performance-Tests wollen wir die Zeit für die Bildschirmausgabe nicht mittesten */
/* println("LCA von " + tag1 + " und " + tag2 + " = " + LCA(tag1, tag2).tag); */
result = LCA(tag1, tag2).tag;
i++;
x--;
}
/* Endzeit nehmen und Ausgabe */
nimmZeit("RMQ-Abfragen");
}
}
/*-----------------------------------------------------------------------------
* Maus auf Mittelposition setzen (innerhalb des Fensters)
*-----------------------------------------------------------------------------*/
mouseX=(screen.width/2);
mouseY=(screen.height/2);
/*-----------------------------------------------------------------------------
* erneute Aufrufe des Events draw() verhindern
*-----------------------------------------------------------------------------*/
if (Zentrierung)
noLoop();
}
void draw()
{
/*-----------------------------------------------------------------------------
* Hintergrundfarbe setzen, dabei wird auch der gesamte Bildschirm gelöscht
*-----------------------------------------------------------------------------*/
background(c3);
/*-----------------------------------------------------------------------------
* Überschriften setzen
*-----------------------------------------------------------------------------*/
fill(c2);
textSize(20);
text("Visualisierung eines binären Suchbaumes (Reingold-Tilford-Algorithmus) in Processing", ((screen.width)/2)-400, 50);
textSize(15);
text("von Thomas Kramer", ((screen.width)/2)-70, 80);
text("(ESC zum Abbrechen)", ((screen.width)/2)-75, 110);
textSize(13);
/*-----------------------------------------------------------------------------
* Baum grafisch ausgeben
*-----------------------------------------------------------------------------*/
if (zeichnen)
{
/* Startzeit nehmen */
completeTimeBefore = System.currentTimeMillis();
ZeigeBaum(Wurzel, 0, 0);
ausgegeben = true;
/* Endzeit nehmen und Ausgabe */
nimmZeit("Baumzeichnen");
}
/*-----------------------------------------------------------------------------
* RMQ-Abfragen beantworten und einzeichnen
*-----------------------------------------------------------------------------*/
if (RMQ_Abfragen)
{
text("Ermittlung des Lowest Common Ancestors anhand der Tags und des RMQ-Algorithmus", ((screen.width)/2)-240, (screen.height)-170);
text("LCA(7,8) = " + LCA(7,8).tag, ((screen.width)/2)-20, (screen.height)-150);
text("LCA(4,6) = " + LCA(4,6).tag, ((screen.width)/2)-20, (screen.height)-130);
text("LCA(3,4) = " + LCA(3,4).tag, ((screen.width)/2)-20, (screen.height)-110);
text("LCA(5,8) = " + LCA(5,8).tag, ((screen.width)/2)-20, (screen.height)-90);
text("LCA(7,9) = " + LCA(7,9).tag, ((screen.width)/2)-20, (screen.height)-70);
}
/*-----------------------------------------------------------------------------
* aktuelle Mauskoordinaten ausgeben
*-----------------------------------------------------------------------------*/
if (!Zentrierung)
{
fill(c3);
rect(1, 0, 80, 60);
fill(c2);
text("x: " + mouseX, 20, 20);
text("y: " + mouseY, 20, 40);
}
}
void berechne_Versatz(tBaum Knoten)
{
/* PostOrder-Druchlauf -> linker Teilbaum, rechter Teilbaum, Wurzel */
if (Knoten!=null)
{
berechne_Versatz(Knoten.links);
berechne_Versatz(Knoten.rechts);
berechne_Konturen(Knoten);
}
}
void berechne_Konturen(tBaum Knoten)
{
/* berechne Konturen, nur notwendig wenn aktueller Knoten zwei Söhne hat */
if (Knoten.links!=null && Knoten.rechts!=null)
{
int linke_Kontur=0;
int rechte_Kontur=0;
/* finde die maximalen Ebenen für die Unterbäume links und rechts, separat */
/* übernimm davon den niedrigeren Wert */
int minLevelinsgesamt=min(Knoten.linksEbenen, Knoten.rechtsEbenen);
/* bestimme den maximalen und minimalen Versatz jeder Kontur bis zu der bestimmten Ebene (einschließlich) */
linke_Kontur = finde_Versatz(Knoten.links, +1, minLevelinsgesamt, (Knoten.links).Versatz);
rechte_Kontur = finde_Versatz(Knoten.rechts, -1, minLevelinsgesamt, (Knoten.rechts).Versatz);
/* Korrigierungs-Versatz berechnen */
int Versatz=((linke_Kontur-rechte_Kontur))+2;
/* Ergebnis ist ungerade? */
if ((Versatz & 1)!=0)
Versatz+=1;
/* Integer-Division */
Versatz=(Versatz>>1);
/* Test-Ausgabe */
if (Versatz <0)
println("abs()-Funktion sollte doch verwendet werden!");
/* diesen Versatz dem linken Teilbaum als negativen Wert aufaddieren, dem rechten Teilbaum
als positiven Wert */
setze_Wert(Knoten.links,-Versatz);
setze_Wert(Knoten.rechts,Versatz);
}
}
/* berechne die Tiefe der jeweiligen Kontur des Knotens */
int finde_Max_Ebene(tBaum Knoten)
{
if (Knoten == null)
return 0;
return max(finde_Max_Ebene(Knoten.links), finde_Max_Ebene(Knoten.rechts)) + 1;
}
/* finde den minimalen/maximalen Versatz für den jeweilig angegebenen
Unterbaum (Kontur) heraus - bis zu einer bestimmten Ebene (einschließlich) */
int finde_Versatz(tBaum Knoten, int Richtung, int biszuEbene, int Versatz)
{
int result=Versatz;
if (Knoten!=null)
{
/* Richtung: -1=suche Minimum, +1=suche Maximum */
if (Richtung==-1)
{
result=min(Knoten.Versatz,result);
} else
{
result=max(Knoten.Versatz,result);
}
/* noch nicht in der letzten zu berücksichtigenden Ebene? */
if (Knoten.Ebene<biszuEbene)
{
result=finde_Versatz(Knoten.links, Richtung, biszuEbene, result);
result=finde_Versatz(Knoten.rechts, Richtung, biszuEbene, result);
}
}
return result;
}
/* addiere den nach der Formel korrigierten Versatz jedem einzelnen
Knoten der angegebenen Kontur auf */
void setze_Wert(tBaum Knoten, int Wert)
{
if (Knoten!=null)
{
Knoten.Versatz+=Wert;
setze_Wert(Knoten.links,Wert);
setze_Wert(Knoten.rechts,Wert);
}
}
/* Einfügen der Knoten, Position wird in der Routine selbst bestimmt */
tBaum Einfuegen(tBaum Knoten, tBaum Vater, int Inhalt, int Versatz, int tag)
{
if (Knoten == null)
{
/* angegebener Knoten existiert noch nicht (Position noch nicht belegt)
--> neuen Knoten erzeugen */
Knoten = new tBaum();
Knoten.Vater = Vater;
Knoten.links = null;
Knoten.rechts = null;
Knoten.Inhalt = Inhalt;
Knoten.Ebene = Ebene+1;
Knoten.tag = tag;
/* Versatz mit Initialisierungswerten versehen */
Knoten.Versatz = Versatz;
if ((Ebene + 1) > EbenenInsgesamt)
EbenenInsgesamt = (Ebene + 1);
/* Position im Baum abhängig zur Wurzel bestimmen */
Knoten.Art=0;
if (Wurzel != null)
{
Knoten.Art = (Inhalt < Wurzel.Inhalt) ? -1 : +1;
/* kleinsten/größten Versatz bestimmen */
if (Knoten.Versatz < (kleinster_Versatz).Versatz)
kleinster_Versatz = Knoten;
if (Knoten.Versatz > (groesster_Versatz).Versatz)
groesster_Versatz = Knoten;
}
letzter_Knoten = Knoten;
} else
{
Ebene += 1;
if (Inhalt < Knoten.Inhalt)
{ /* kleineren Wert als den des aktuellen Knotens immer als linken Sohn einfügen */
Knoten.links = Einfuegen(Knoten.links, Knoten, Inhalt, Versatz-1, tag);
Knoten.linksEbenen = max(Knoten.linksEbenen, letzter_Knoten.Ebene);
}
else if (Inhalt > Knoten.Inhalt)
{ /* größeren Wert als den des aktuellen Knotens immer als rechten Sohn einfügen */
Knoten.rechts = Einfuegen(Knoten.rechts, Knoten, Inhalt, Versatz+1, tag);
Knoten.rechtsEbenen = max(Knoten.rechtsEbenen, letzter_Knoten.Ebene);
}
Ebene -= 1;
}
return Knoten;
}
/* Baum visuell ausgeben */
void ZeigeBaum(tBaum Knoten, int StartPosKanteLinks, int StartPosKanteOben)
{
if (Knoten == null)
return;
if (!ausgegeben)
{
Knoten.Versatz += GesamtVersatz;
}
int GesamtPositionLinks = 0;
int GesamtPositionLinks_2 = 0;
int GesamtPositionOben = 0;
int GesamtPositionOben_2 = 0;
int Zentri_Space = 0;
int BenutzteFelder = (Knoten.Versatz - 1) * (Breite + ZwischenAbstandLinks);
boolean Fehler = false;
if (Zentrierung)
{
Zentri_Space = (screen.width - AbstandLinks - MaxElementePlatz) / 2;
GesamtPositionLinks = Zentri_Space + AbstandLinks + BenutzteFelder;
GesamtPositionOben=AbstandOben + (Knoten.Ebene * Hoehe) + (Knoten.Ebene * ZwischenAbstandOben);
}
else {
GesamtPositionLinks=((screen.width / 2) - mouseX) - AbstandLinks + BenutzteFelder;
GesamtPositionOben=((screen.height / 2) - mouseY) - AbstandOben + (Knoten.Ebene * Hoehe) + (Knoten.Ebene * ZwischenAbstandOben);
}
GesamtPositionLinks_2 = GesamtPositionLinks + Breite_2;
GesamtPositionOben_2 = GesamtPositionOben + Hoehe_2;
/* Erkennen, ob schon ein Knoten an die Stelle gezeichnet wurde */
color cp = get(GesamtPositionLinks + 1, GesamtPositionOben + 1);
if (cp == c2)
{
println("Fehler! Es wurde schon ein Knoten an diese Stelle gezeichnet!");
println("betreffend Knoten: " + Knoten.Inhalt);
Fehler = true;
}
/* Rahmen zeichnen */
if (Fehler)
fill(c4);
else
fill(c2);
rect(GesamtPositionLinks,
GesamtPositionOben,
Breite,
Hoehe);
/* Inhalte einzeichnen */
fill(c1);
text(Knoten.Ebene+". Ebene=" +Knoten.Inhalt + ", tag " + Knoten.tag,
GesamtPositionLinks + 5,
GesamtPositionOben + 15);
line(GesamtPositionLinks,
GesamtPositionOben_2,
GesamtPositionLinks + Breite,
GesamtPositionOben_2);
line(GesamtPositionLinks_2,
GesamtPositionOben_2,
GesamtPositionLinks_2,
GesamtPositionOben + Hoehe);
if (Knoten.links != null)
text((Knoten.links).Inhalt,
GesamtPositionLinks + 5,
GesamtPositionOben_2 + 15);
if (Knoten.rechts!=null)
text((Knoten.rechts).Inhalt,
GesamtPositionLinks_2 + 5,
GesamtPositionOben_2 + 15);
if (Knoten.Ebene != 1)
line(StartPosKanteLinks, StartPosKanteOben, GesamtPositionLinks_2, GesamtPositionOben);
/* Rekursionsaufrufe */
if (Knoten.links != null)
ZeigeBaum(Knoten.links, GesamtPositionLinks_2, GesamtPositionOben + Hoehe);
if (Knoten.rechts != null)
ZeigeBaum(Knoten.rechts, GesamtPositionLinks_2, GesamtPositionOben + Hoehe);
}
/* Startwert sollte bei -1 liegen */
int Euler_Tour(tBaum Knoten, int Zaehler)
{
if (Knoten!=null)
{
Zaehler+=1;
RMQ_E[Zaehler]=Knoten;
RMQ_L[Zaehler]=Knoten.Ebene-1;
if (Knoten.links!=null)
{
Zaehler=Euler_Tour(Knoten.links, Zaehler)+1;
RMQ_E[Zaehler]=Knoten;
RMQ_L[Zaehler]=Knoten.Ebene-1;
}
if (Knoten.rechts!=null)
{
Zaehler=Euler_Tour(Knoten.rechts, Zaehler)+1;
RMQ_E[Zaehler]=Knoten;
RMQ_L[Zaehler]=Knoten.Ebene-1;
}
}
return Zaehler;
}
/* fülle Repräsentanten-Array, welche das erste Vorkommen jedes Knotens enthält */
void fillRMQ_R_Array()
{
/* RMQ_R füllen. Dazu alle Knoten durchgehen... */
int s=0;
for (int r=0; r<Baumelemente; r+=1)
{
/* ... und für jeden Knoten den ersten Eintrag im RMQ_E-Array finden ... */
for (s=0; s<(Baumelemente*2-1); s+=1)
{
if (RMQ_E[s].tag == r)
break;
}
RMQ_R[r]=s;
}
}
/* mittels RMQ-Algorithmus den Lowest Common Ancestor ermitteln */
tBaum LCA(int tag1, int tag2)
{
/* Suche im RMQ_R-Array zunächst die Entsprechung für tag1 und tag2 der beiden
ausgewählten Knoten aus, suche dann innerhalb dieser Grenzen im RMQ_L-Array
den niedrigsten Wert heraus.
Anschließend wird im RMQ_E-Array der Wert aus dieser Indexposition zurückgegeben */
int lowest=Baumelemente;
int lowest_index=0;
tBaum result=null;
for (int i=min(RMQ_R[tag1], RMQ_R[tag2]); i<=max(RMQ_R[tag1], RMQ_R[tag2]); i+=1)
{
if (RMQ_L[i]<lowest)
{
lowest=RMQ_L[i];
lowest_index=i;
}
}
/* Default-Rückgabewert setzen gemäß Algorithmus */
result = RMQ_E[lowest_index];
/* wenn Knoten B ein Sohn von A ist wird A gemäß Algorithmus zurückgeliefert,
dann greift Ausnahmeregelung */
if ((RMQ_E[lowest_index].tag == tag1) || (RMQ_E[lowest_index].tag == tag2))
if (RMQ_E[lowest_index].Vater != null )
result = RMQ_E[lowest_index].Vater;
return result;
}
/* Zeitmessung ausgeben, completeTimeBefore muss vorher separat genommen werden */
void nimmZeit(String AusgabeString)
{
completeTimeAfter = System.currentTimeMillis();
completeTimeDiff = completeTimeAfter - completeTimeBefore;
/* Ausgabe für Gesamtdurchlauf formatieren */
String timeString = String.format("\n\nZeit benötigt für %s: %02d min, %02d sec, %03d milliseconds",
AusgabeString,
TimeUnit.MILLISECONDS.toMinutes(completeTimeDiff),
TimeUnit.MILLISECONDS.toSeconds(completeTimeDiff) -
TimeUnit.MINUTES.toSeconds(TimeUnit.MILLISECONDS.toMinutes(completeTimeDiff)),
completeTimeDiff % 1000);
println(timeString);
}